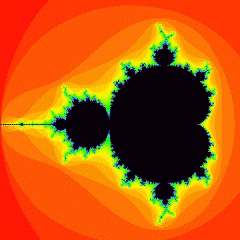
Fig. 1: the entire Mandelbrot Set.

The Mandelbrot set is a collection of points in the complex plane.  In Figure 1, the black areas are points inside the set, while colored areas are outside it.  As you can see, it has a jagged, spiky appearance.  In fact, the boundary of this set, the edge where the black and colored areas meet, is infinitely detailed. What does this mean?

Although the set's boundary is a continuous curved line, and it fits into a finite area (the entire Mandelbrot Set is within the circle of radius 2 around the origin of the plane), the boundary nevertheless has infinite length.  This is another common property of fractal objects; their boundaries have infinite length (if they are 2D) or area (if they are 3D).  To see how this is possible, consider a coastline.

Suppose you had a coastline and two points on it, and you want to measure the distance along the coast between the points.  Obviously, the shortest distance between the points would be a straight line; but suppose instead of measuring a straight line, you measured more accurately along the coastline.  You would probably get quite a bit larger distance, unless the coastline was exceptionally straight.  Now zoom in closer and measure the distance along the coastline even more accurately, and the distance between the two points increases again.  You can imagine that you could keep zooming in until you were crawling along the beach with a microscope, painstakingly measuring the distance around each and every grain of sand.  Clearly, as you measure more and more accurately in this way, the distance from one point to the other along the coastline approaches infinity very rapidly.

Of course, the length of the coastline can never be actually infinite—the amount of detail in it is limited by the size of the atoms that make up the sand along the beach.  But a mathematical fractal is not limited by the size of atoms.  The length of the edge of a fractal like the Mandelbrot set is truly infinite, but all this infinite length is packed into a finite area—forcing the boundary to contain details at all levels of scale.  You can keep zooming into the Mandelbrot set forever, and you will never come to the end.