LUA is a scripting language mainly designed to be integrated in host applications. It is the perfect tool to learn the basics of programming since it contains all the elements which are present in all the other programming languages. The host application which will make it possible to run the LUA code in real situation is Demoniak3D. But we will also use the lua.exe interpreter for an immediate and simple command line use.

Links:

• LUA home page: the official website of LUA.
• LUA.exe: LUA command line interpreter.
• XpConfigurator: the utility which makes it possible to add a menu to open a DOS shell on a mouse right clic. This is useful to test LUA codes with the command line interpreter.

But before starting, we will make the traditional "Hello World", in order to check if the interpreter works properly. You just have to copy the following code in a file which you will call hello.lua:

print("Hello World From LUA!");

Code 1 - Hello World!
Put this file in the same repertory that lua.exe and open a Shell in the directory of the interpreter. Now you can run this first script following the order:

lua hello.lua

If every thing is ok, the result must be the one of figure 1:


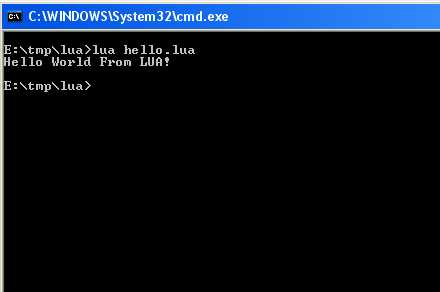
Fig. 1 - Your first LUA script
To write LUA code, you need a text editor (not a word processing software!). Here is a small selection of some free and commercial editors:

• Notepad++: simple, powerful, free and regularly updated. Syntaxic colouring for the main programming languages (LUA, XML, C/C++ HTML, VBS, Java...).
• Crimson Editor: simple, powerful and free. The updates are not very frequent. Syntactic colouring for most programming languages.
• Ultra-Edit: a very powerful text editor. Paying (approximately 40.00$).

The variable is one of the most fundamental programming concept. A rather general variable definition could be: memory location for data storage.

Like in many scripting languages (PHP, VBScript...), the variables in LUA are typeless. That means that a variable can contain a numerical value as well a string character, or even a variable (simple or complex).

Moreover, no declaration is requuired before using a variable. It may directly be used. It is simple but this can sometimes leads to some problems when coding large scripts. It would really have been appreciated if the language could offer the possibility to activate an option that forces the variables declaration before using them. Here is a very simple example:

a = 10;
b = 3;
sum = a + b;
print("Sum = " .. sum );

Code 2 - Adder
Run it, the result must be:


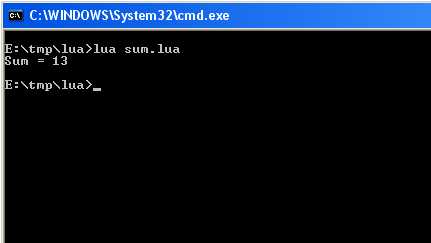
Fig. 2 - the adder in action.

Another point that must be considered is the variables visibility range. By default, variables in LUA are global variables. It means that variables can be used in various scripts, when these various scripts belong to the same execution context, as it is the case in the Demoniak3D demonstrations (initialization script, update script...). The global variables are thus very useful in all the cases where one needs to transfer data between various scripts, or when persistent data are required. We will see a "frames counter" example in one of the tutorials devoted to the use of LUA in Demoniak3D.

If you need to limit the range of a variable, you just have to add the local key word (language reserved word) in front of the variable:

a = 10;
local b = 3;
sum = a + b;
print("Sum = " .. sum );

Code 3 - Creation of a local variable
The variables which we have just seen are simple variables, in the sense that they contain simple values (a number and/or a string character). In many cases, depending of course on the algorithms and the abstraction level, we need to define more sophisticated variables. A simple example is the handling of 3d vectors. In this case, it is simpler to handle only one variable containing the 3 components of the vector, rather than to handle 3 variables representing each one a component. The creation of a variable which would let us act on 3D vectors can be done the following way:

vecA = {x=2.0, y=-1.0, z=0.0};
vecB = {x=-4.0, y=0.0, z=-2.0};	
vecSum = vecB;
vecSum.x = vecA.x + vecB.x;
vecSum.y = vecA.y + vecB.y;
vecSum.z = vecA.z + vecB.z;

Code 4 - Creation of complex variables
Another category of variables usually used is the table. A table can be defined as a set of variables which can be reached by an index. A table is refered with the [] symbol. Each value contained in a cell of the table is called element. The following code gives an example:

-- Array creation.
myArray = {}; 

-- Array initialization.
myArray[0] = 10.0;
myArray[1] = 20.0;
myArray[3] = "Hello";
vecA = {x=-4.0, y=0.0, z=-2.0};	
myArray[4] = vecA;

Code 5 - Creation and initialization of a table

LUA, like any other good programming language, gives the possibility to create functions. A function can be considered as a sequence of instructions masked behind a single name and making it possible to execute an action or to act on data. A function simply makes it possible to factorize the code in order to avoid coding several times the same succession of instructions.

In LUA there are 2 categories of functions:

• Existing functions: LUA standard libraries - such as the print() function.
• User functions: created by the developer

The interesting case is the user functions one.

Let us take again our addition of presently but, now, create a function to add 2 numbers. This function will add the 2 numbers and will display the sum:

function add( a, b)
	local sum = a + b;
	print( "Sum = " .. sum );
end

add(12, 45);
add(548.02, 14587.2298);
add(-1, 1);

Code 6 - Creation of a function
A function can also return a value. Let us slightly modify our adder so that it returns the sum of the 2 last numbers that are passed as parameter:

function add( a, b)
	local sum = a + b;
	return(sum);
end

local sum = add(12, 45);
sum = add(548.02, 14587.2298);
sum = add(-1, 1);

Code 7 - Creation of an addition function
The returned variable can be a simple or a complex one as shown in the following example:

function createVec(_x, _y, _z)
	local out = {x = _x, y = _y, z = _z};
	return(out);
end

function addVec( u, v )
	local out = {x=0.0, y=0.0, z=0.0};
	out.x = u.x + v.x;
	out.y = u.y + v.y;
	out.z = u.z + v.z;
	return(out);
end

function printVec( v )
	print( "vector: <" .. v.x .. ", " .. v.y .. ", 
	       " .. v.z .. ">" );
end

local vecA = createVec(0.22, 0.45, -0.66);
local vecB = createVec(-012, 0.55, 0.59);
local vecSum = addVec(vecA, vecB);
printVec( vecSum );

Code 8 - Creation of a complex function
The execution of code 8 gives the following result:


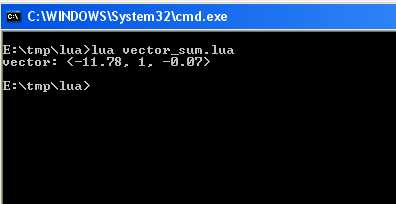
Fig. 3 - Addition of vectors.

The sequencing of data is the technical term which includes all the logic that controls the data flow. This mainly includes:

• the conditional tests structures
• the iterative structures

The conditional tests are done with the if - then - else construction. A simple example which clearily shows the conditional tests may be the solving of the quadratic equation: ax^2 + bx + C = 0.

The following code applies the traditional algorithm (calculation and test of the determinant) to solve the equation:

--
-- Solving of the quadratic equation: ax^2 + bx + c =0
--

text = "";
a = 2.0;
b = 1.0;
c = -2.0;

print( "\nEquation " .. a .. "x^2 + " .. b .. "x +
       " .. c .. " = 0\n" );

-- 1)  Determinant calculus
--
delta = b*b - (4 * a * c );

-- 2)  Solutions depending on the determinant
--
if( delta<0 ) then
	text = "There is no real solution."
elseif( delta == 0 ) then
	x = -b / (2 * a);
	text = "There is one real solution: x=" .. x;
else
	x1 = (-b + math.sqrt(delta)) / (2*a);
	x2 = (-b - math.sqrt(delta)) / (2*a);
	text = "There are two real solutions: x1=" .. x1 .. " 
	       et x2=" .. x2;
end

print( text );

Code 9 - Resolution of the quadratic equation
You just have to test this code...



The iterative structures make it possible to repeat a sequence of operations several times. The iterations are done with while / do-while / repeat-until / for.

The following example shows how to calculate the sum of the first 100 integers using iterators:

sum = 0;
loop_counter = 0;
limit_sup = 100;
while( loop_counter<limit_sup ) do
	sum = sum + loop_counter;
	loop_counter = loop_counter + 1;
	print( "Intermediate sum = " .. sum );
end

print( "
The sum of the " .. limit_sup .. " first integers is: " .. sum );

Code 10 - Sum of the first 100 integers


The following example shows how to use a for loop:

for j=0,10 do
	for i=0,10 do
		print( "j=" .. j .. " i=" .. i );
	end
end	

Code 11 - The for loop
It is possible to prematurely leave an iteration with the break key word.

To end this LUA initiation, here is a complete example which uses all that we've seen until now: LUA implementation of the famous bubbles sort algorithm. The script is divided into 3 parts:

• Part 1: creation of a table containing MAX_SIZE elements. The value of each element is randomly generated thanks to the random() function of the LUA standard math library.
• Part 2: sorting in descending order the elements of the table using the bubbleSort algortihm.
• Part 3: display of the sorted elements.

-- 1) creation and initilisation of a table
--
myArray = {};
MAX_SIZE = 10;
i = 0;
while( i<MAX_SIZE ) do
	myArray[i] = math.random(200);
	print( "myArray[" .. i .. "]=" .. myArray[i] );
	i = i + 1;
end

-- 2) sorting the array with the bubbleSort algorithm
--
num_swaps = 0;
i = 0;
while( i<MAX_SIZE ) do 
	j = i+1;
	while( j<MAX_SIZE ) do 
		if( myArray[j] > myArray[i] ) then
			tmp = myArray[j];
			myArray[j] = myArray[i];
			myArray[i] = tmp;
			num_swaps = num_swaps + 1;
		end
		j = j + 1;
	end
	i = i + 1;
end

-- 3) display of the sorted array
--
print( "
And here is the sorted array:
" );
i = 0;
while( i<MAX_SIZE ) do
	print( "myArray[" .. i .. "]=" .. myArray[i] );
	i = i + 1;
end

print( "\nthere has been " .. num_swaps .. " swaps to sort 
      this array" );

Code 12 - Bubbles Sort
The execution of code 12 gives the following result:


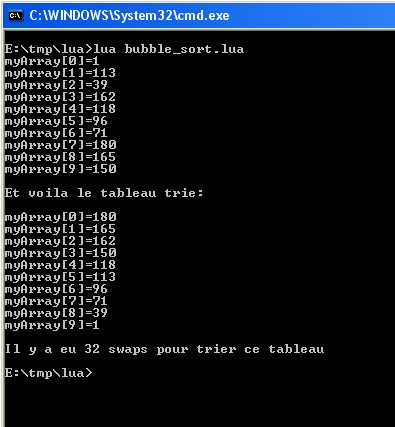
Fig. 4 - Bubbles Sort.

Coding Conventions are very significant and even essential to get clear code, functional, easy to read and especially EASY TO DEBUG! Each one is free to adopt any coding conventions he likes, the main thing being to reach the previously quoted objectives. Personnaly, here are the coding principles that I use:

• Prefix the name of the global variables with g_. Example: g_frame_counter = 0;
• Always add a semicolon at the end of each instruction. Indeed, LUA is very flexible and does not oblige to specify in an explicit way the end of an instruction. But it is recommended to do it in order to simplify the work of the LUA parser / compiler.
• Correctly indent the code and respect the identation hierarchies. See the bubbles sort algorithm for an example.
• Name in an explicit way the variable and the functions. This is fundamental for the reading and the undestanding of a complex code. It is easier to understand the meaning of a variable called g_position_sphere_red_x rather than x1...
• Prefix a table type variable with arr. Example: Arr_sphere_clones or g_arr_sphere_clones if the variable is a global one.
• Prefix a variable with I, F or str to indicate if it contains an integer numerical value (I), real (f) or a character string (str). Example: g_i_status, str_name, g_f_position_x.
• Put comments (--). Comments have a triple role: they give a progress report on what is beeing coded, they show what has been coded and finally they show other developpers what the previous developper tried to code...